Optimizer
Optimizer는 딥러닝에서 Network가 빠르고 정확하게 학습하는 것을 목표로 한다. 주로 Gradient Descent Algorithm을 기반으로한 SGD에서 변형된 여러종류의 Optimizer가 사용되고 있다.
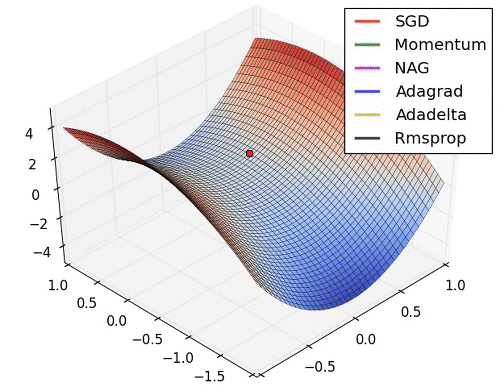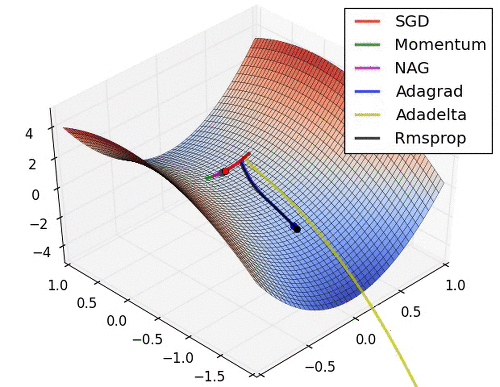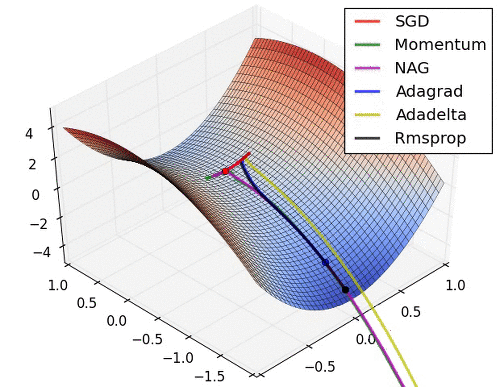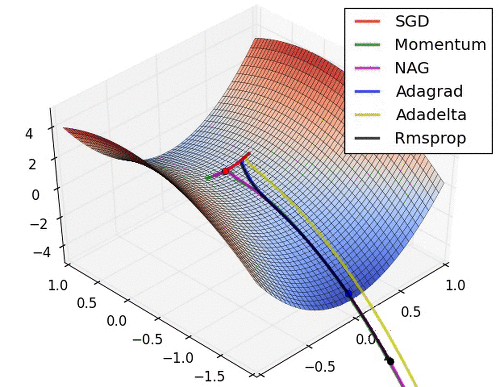
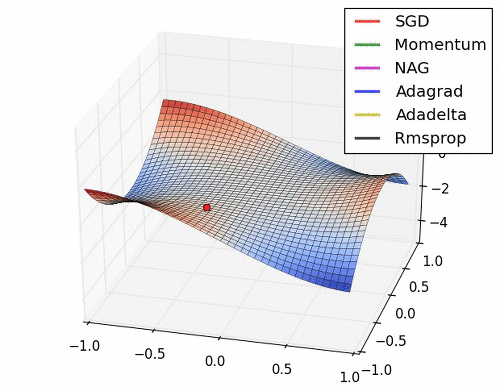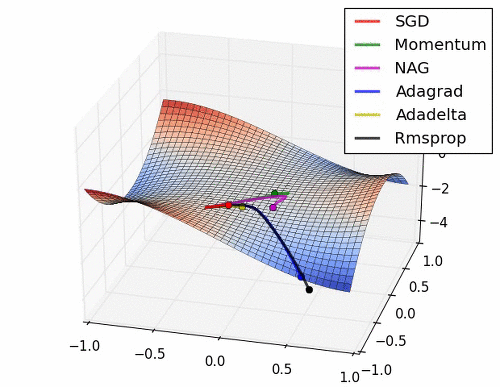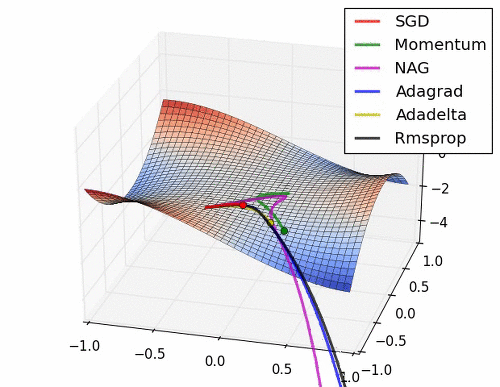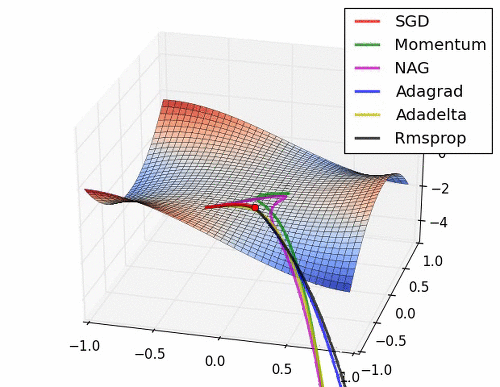
아래는 대표적인 Optimizer 기법들이 최적값을 찾아가는 그래프로 각각의 특성이 잘 드라나 있다.

초기 SGD는 고정된 learning rate에 의해 동일한 스텝으로 학습되기 때문에 느린 학습속도를 보여준다. 하지만, 학습과정에서 안정성이 가장 높은 기법이라고 할 수 있다.
관성을 이용한 Momentum과 NAG는 학습이 충분히 되지 않았다면 SGD와 비교했을 때, 매우 안좋은 성능을 보여줄 수 있다.
아래부터는 각 기법에 따른 특징과 update방식을 정리한다.
Momentum
위 그래프에서 보다싶이 SGD는 다른 기법에 비해 매우느리다.(BGD가 느려서 mini batch로 구분했지만…)
위와 같이 기울기 값이 이전과 동일하다면 step의 길이도 동일하게 update된다.
또한, 기울기 값이 0이되는 지점에서 update가 되지않기 때문에 global이 아닌 local minima에 수렴할 수 있다.

Momentum은 빠른학습속도와 local minima를 문제를 개선하고자 SGD에 관성의 개념을 적용했다.
는 이전 이동거리와 관성계수 에 따라 parameter를 update하도록 수식이 적용되었다.
일반적으로 관성계수 은 0.9를 사용한다.
관성개념이 적용되어 수렴되는 최적 parameter를 더욱 빠르게 학습할 수 있으며 gradient값이 0인 곳에서도 관성에 의해 업데이트가 수행될 수 있다.
Nesterov Accelrated Gradient (NAG)
Momentum은 현재 update과정에서의 기울기 값을 기반으로 미래값을 도출하도록 되어있다. 따라서, 최적의 parameter를 관성에 의해 지나칠 수 있게 된다.
NAG에서는 Momentum으로 이동된 지점에서의 기울기를 활용하여 update를 수행하기 때문에 이러한 문제를 해소할 수 있게 된다.
위 NAG의 update 식에서도 와 같이 관성에 의해 이동된 곳에서의 기울기를 적용하는것을 볼 수 있다. 이는 관성에 의해 빨리 이동하는 이점을 누리면서도 멈춰야하는 곳에서 효과적으로 제동할 수 있게 된다.
Adaptive Gradient (Adagrad)
Adagrad에서는 동일 기준으로 update되던 각각의 parameter에 개별 기준을 적용하였다.
즉, 지속적으로 변화하던 parameter는 최적값에 가까워졌을것이고 한 번도 변하지 않은 parameter는 더 큰 변화를 줘야한다는 것이 Adagrad의 개념이다.
Adagrad의 update 수식은 아래와 같다.
는 Network의 parameter수 k차원의 벡터로 이동한 거리를 나타내는 척도로 사용되어 Gradient의 sum of squares를 저장하고 있다. 이후 parameter update시 learning rate에 반비례로 적용되어 높은 값을 가지는 parameter에서는 상대적으로 적은 변화를 주고 반대로 적게 이동한 parameter에서는 큰 변화를 주게 된다.
은 작은 값으로 0으로 나누어지는 것을 방지하기 위해 사용된다.
Adagrad에도 단점이 있다. parameter별 상대적인 변화로 update를 수행하는 개념은 좋았으나 학습이 진행됨에 따라 변화 폭이 눈에 띄게 줄어들어 결국 움직이지 않게 된다.
RMSProp
Adagrad에서 문제점을 개선하기 위해 계산식에 지수이동평균을 적용하였다. 이로인해 학습의 최소 step은 유지할 수 있게 된 셈이다.
update 식은 다음과 같다.
는 지수이동평균 필터링에서 보통 forgetting factor, decaying factor라 불리며 hyperparameter로 0.9~0.999의 값을 취한다.
식에서와 같이 학습이 진행됨에 따라 parameter사이 차별화는 유지하되 학습속도가 지속적으로 줄어들어 0에 수렴하는 것은 방지 할 수 있게 된다.
Adaptive Delta (Adadelta)
RMSProp과 같이 Adagrad의 개선을 위해 제안된 방법이다. 계산식은 RMSProp과 동일하게 수행되지만, update과정에서 learning rate를 사용하는 대신 이를 대신하는 무언가가 추가되었다…(momentum와 비슷해 보이지만 뭔가 다른느낌)
식을 보면 지수이동평균이 적용된 와에 의해 step의 크기가 결정되도록 되어있다. 이는 Second-order optimization을 approximate하기 위함이라지만 공부가 필요할 듯하다.
Adaptive Moment Estimation (Adam)
RMSProp와 Momentum 기법을 합친 optimizer. Momentum에서 관성계수 과 함께 계산된 로 parameter를 업데이트하지만 Adam에서는 기울기 값과 기울기의 제곱값의 지수이동평균을 활용하여 step변화량을 조절한다.
hyperparameter는 각각 , , 의 값들이 추천된다.
Adam에서는 초기 몇번의 update에서 0으로 편향되어 있어 이를 보정하는 매커니즘이 반영되어있다.
'Algorithm > Deep Learning' 카테고리의 다른 글
| Gradient Descent Algorithm (0) | 2020.05.05 |
|---|